Lineare Gleichungssysteme

Lineare Gleichungssysteme werden zur Berechnung auf Dreiecksform (wird auch erweiterte Koeffizientenmatrix genannt) gebracht und mithilfe des Gauß - Algorithmus / Gaußsche Eliminationsverfahren gelöst.

Arten von Gleichunssystemen:

• überbestimmte lineare Gleichungssysteme
• unterbestimmte lineare Gleichungssysteme (keine eindeutige Lösung, sondern Vereinfachung der Abhängigkeit)

Ein Beispiel:

I      X1 + X2 - X3 = 1
II    X1 - X2 + X3 = 1
III   X1 + X2 + X3 = 1


1. Schritt

• Tabelle in Form bringen (Variablen X1 usw. werden ausgeblendet)

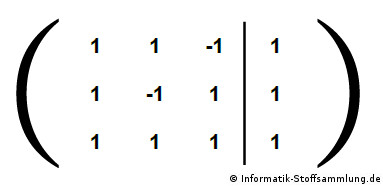
2. Schritt

• durch Umformung / Elimination / Vertauschen
• auf Dreiecksform bringen

3. Schritt

• Variablen auslesen und in weitere Zeilen einfügen

aus der letzten Zeile der oberen Grafik:
--->   -2X3 = 0   --->   X3 = 0

jetzt wird die soeben gewonnene Variable X3 in die zweite Zeile der oberen Grafik eingesetzt und wir erhalten:
(bei diesem Beispiel ist das Einsetzen garnicht nötig da die Variable in der zweiten Zeile nicht vorhanden ist)
--->   2X2 = 0   --->  X2 = 0

nun setzen wir X3 und X2 in die erste Zeile ein:
--->   X1 + X2 - X3   --->   X1 = 1


4. Schritt

• Lösungsmenge definieren