Matrizenkalkül

Eine Matrix besteht aus Spalten und Zeilen.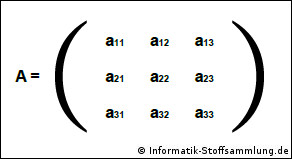

Eigenschaften von Matrizen

• 2 Matrizen sind gleich wenn das Format gleich ist (d. h. gleich viele Spalten und gleich viele Zeilen)
• um von der Matrix zur transponierten Matrix zu gelangen werden die Zeilen zu Spalten und die Spalten werden zu Zeilen
• bei quadratischen Matrizen ist das Transponieren gleich dem Spiegeln an der Hauptdiagonale (links oben nach rechts unten)
• Matrizen heißen symetrisch wenn: Matrix = transponierte Matrix   ( A = A^T )
• Matrizen mit einer Spalte werden auch Spaltenvektoren genannt
• eine Einheitsmatrix ist immer quadratisch und nur auf der Hauptdiagonale Einsen, sonst nur Nullen

Matrix addieren und subtrahieren

1.  Matrix + Matrix
(Bild)

2.  Matrix - Matrix
(Bild)

3.  Matrix + Spaltenvektor
(Bild)

4.  Matrix - Spaltenvektor
(Bild)

Matrix multiplizieren (Matrix, Spaltenvektor)

1. Matrix und Spaltenvektor
(Bild)

2. Matrix und Matrix
(Bild)

Matrix invertieren

1. Prüfen ob die Matrix eine quadratische Matrix ist mithilfe der Berechnung der Determinante
2. zu invertierende Matrix in Einheitsform bringen (Einheitsmatrix siehe Bild; links Matrix, rechts Einheitsmatrix)

(Bild)
3.  nach der Umformung sehen wir auf der linken Seite die Einheitsmatrix und auf der rechten Seite die gesuchte inverse Matrix
(Bild)

Determinante berechnen

Bei 2 * 2 Matrix

det(A) = a11 * a22  -  a12 * a21

1. Schritt
2. Schritt


Bei 3 * 3 Matrix

det(A) = (a11 * a22 * a33  -  a31 * a22 * a13)   +   (a12 * a23 * a34  -  a32 * a23 * a14)   +   (a13 * a24 * a35  -  a33 * a24 * a15)

1. Schritt
2. Schritt